题目内容
一个圆柱体和一个圆锥体的体积相等,它们底面半径的比是2:3,圆柱的高是18厘米,圆锥的高是________厘米.
24
分析:设圆锥的半径为r,圆锥的高为h,则圆柱的半径为 r,圆柱的高18厘米,则依据圆柱的体积=底面积×高,圆锥的体积=
r,圆柱的高18厘米,则依据圆柱的体积=底面积×高,圆锥的体积= ×底面积×高,即可求出圆锥的高.
×底面积×高,即可求出圆锥的高.
解答:设圆锥的半径为r,圆锥的高为h,则圆柱的半径为 r,
r,
则 πr2h=π
πr2h=π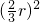 ×18
×18
 πr2h=π
πr2h=π r2×18,
r2×18,
 h=8,
h=8,
h=24;
答:圆锥的高是24厘米.
故答案为:24.
点评:此题主要考查圆柱与圆锥的体积的计算方法,关键是利用假设法弄清楚二者的半径的关系.
分析:设圆锥的半径为r,圆锥的高为h,则圆柱的半径为
 r,圆柱的高18厘米,则依据圆柱的体积=底面积×高,圆锥的体积=
r,圆柱的高18厘米,则依据圆柱的体积=底面积×高,圆锥的体积= ×底面积×高,即可求出圆锥的高.
×底面积×高,即可求出圆锥的高.解答:设圆锥的半径为r,圆锥的高为h,则圆柱的半径为
 r,
r,则
 πr2h=π
πr2h=π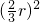 ×18
×18 πr2h=π
πr2h=π r2×18,
r2×18, h=8,
h=8,h=24;
答:圆锥的高是24厘米.
故答案为:24.
点评:此题主要考查圆柱与圆锥的体积的计算方法,关键是利用假设法弄清楚二者的半径的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个封闭的容器由一个圆柱体和一个圆锥组成,如图所示,其内放有一些水,圆锥在上的时候水面高度是12厘米,倒放时,水面高度是20厘米,那么这个容器圆锥部分的高是
一个封闭的容器由一个圆柱体和一个圆锥组成,如图所示,其内放有一些水,圆锥在上的时候水面高度是12厘米,倒放时,水面高度是20厘米,那么这个容器圆锥部分的高是