Question

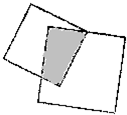
如图，两个正方形边长分别是10和6，阴影部分的面积

40.26

．

Answer 1

分析：连接BD，AE，则阴影部分的面积等于三角形ABD的面积+扇形EBD的面积-三角形EBD的面积，所以根据等底等高的三角形的面积相等，得出三角形ABD的面积等于三角形ABE的面积，进而根据三角形的面积公式与圆的面积公式解决问题．

解答：解：如图连接BD，AE，

因为三角形ABD与三角形AEB等底等高，所以三角形ABD的面积是：10×6÷2=30，
三角形BED的面积是：6×6÷2=18，
扇形EBD的面积是：

1

4

×3.14×6²，
=3.14×9，
=28.26，
阴影部分的面积：30+28.26-18=40.26，
答：阴影部分的面积是40.26，
故答案为：40.26．

点评：关键是将阴影部分的面积进行分割，再利用相应的公式分别求出各个部分的面积即可．