题目内容
 圆柱形的售报亭的高与底面直径相等,如图所示,开有一个边长等于底面半径的正方形售报窗口.问:窗口处挖去的圆柱部分的面积占圆柱侧面面积的几分之几?
圆柱形的售报亭的高与底面直径相等,如图所示,开有一个边长等于底面半径的正方形售报窗口.问:窗口处挖去的圆柱部分的面积占圆柱侧面面积的几分之几?分析:如图:设底面圆的半径为R.∠AOB=60°,弧AB为圆周长的
,所以圆柱侧面ABCD部分为整个圆柱侧面的
,而窗口高为R是圆柱高2R的一半,所以窗口部分挖去的圆柱面部分的面积是圆柱侧面面积的
.由此得解.
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 12 |
解答: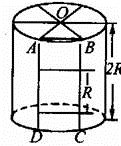 解:设底面圆的半径为R.由图可见,三角形OAB是等边三角形,.∠AOB=60°,弧AB为圆周长的
解:设底面圆的半径为R.由图可见,三角形OAB是等边三角形,.∠AOB=60°,弧AB为圆周长的
,所以圆柱侧面ABCD部分为整个圆柱侧面的
,而窗口高为R是圆柱高2R的一半,所以窗口部分挖去的圆柱面部分的面积是圆柱侧面面积的
.事实上也可以直接计算:
窗口柱面挖去面积:s1=
2πR×R=
πR2,
圆柱侧面面积:s=2πR×2R=4πR2,
所以
=
=
;
答:窗口处挖去的圆柱部分的面积占圆柱侧面面积的
.
 解:设底面圆的半径为R.由图可见,三角形OAB是等边三角形,.∠AOB=60°,弧AB为圆周长的
解:设底面圆的半径为R.由图可见,三角形OAB是等边三角形,.∠AOB=60°,弧AB为圆周长的| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 12 |
窗口柱面挖去面积:s1=
| 1 |
| 6 |
| 1 |
| 3 |
圆柱侧面面积:s=2πR×2R=4πR2,
所以
| S1 |
| S |
| ||
|
| 1 |
| 12 |
答:窗口处挖去的圆柱部分的面积占圆柱侧面面积的
| 1 |
| 12 |
点评:此题主要考查圆柱的侧面积公式的灵活运用,由窗口边长等于底面半径推出圆柱的高是底面半径的2倍,进而根据圆柱的侧面积公式解答.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目