Question

15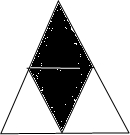．如图是由4个边长为6厘米的等边三角形拼成的大三角形．
（1）图中一共有3个梯形，每个梯形的内角和都是360°．
（2）涂色四边形中的一个钝角是120°，拼成的大三角形的周长是其中一个小三角形周长的2倍．

Answer 1

分析 （1）根据梯形的特点，只有一组对边平行的四边形是梯形，由此找出图形中的梯形，每个梯形可以分成2个三角形，所以每个梯形的内角和是三角形内角和的2倍，即180°×2；
（2）小三角形是等边三角形，每个内角都是60°，涂色四边形的一个钝角和三角形的一个内角构成一个平角，用平角的度数减去60°就是一个四边形内角的度数；拼成的大三角形也是一个等边三角形，它的边长是两个小三角形的边长，由此求出大三角形的边长，进而分别求出大小三角形的周长，再用大三角形的周长除以小三角形的周长即可．

解答 解：（1）观察图发现，图中一共有3个梯形；
每个梯形可以分成2个三角形，如图：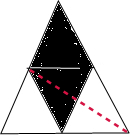

因为三角形的内角和是180°，所以梯形的内角和是：180×2=360（度）；

（2）180-60=120（度）
6×2×3=36（厘米）
6×2=18（厘米）
36÷18=2
所以：涂色四边形中的一个钝角是 120°，拼成的大三角形的周长是其中一个小三角形周长的 2倍．
故答案为：3，360，120，2．

点评 本题综合性较强，综合考查了梯形的特点，三角形的内角和，平角的度数，以及三角形周长等有关知识，要注意逐题分析，找清楚它们之间的联系，再进行求解．