题目内容
(2011?云霄县)请按要求操作.
①通过测量,点A在点B的东偏北
②把三角形ABC平移,使平移后的图形与图中的长方形组成一个轴对称图形,并画出这个组合图形的对称轴.
③画出长方形绕点O顺时针旋转90°后的图形,点D旋转后的对应位置用数对可表示为
④按1:2的比画出这个三角形缩小后的图形,新图形与原来图形的面积比是

①通过测量,点A在点B的东偏北
65
65
度,请判断∠C=65
65
度.②把三角形ABC平移,使平移后的图形与图中的长方形组成一个轴对称图形,并画出这个组合图形的对称轴.
③画出长方形绕点O顺时针旋转90°后的图形,点D旋转后的对应位置用数对可表示为
(11,2)
(11,2)
.④按1:2的比画出这个三角形缩小后的图形,新图形与原来图形的面积比是
1:4
1:4
.
分析:(1)根据测量角的方法,先测量出∠B的度数,再利用方向标,以点B为观测中心,即可表示点A的位置;由图形可知,这个三角形是等腰三角形,所以∠C的度数就等于∠B的度数;
(2)根据轴对称图形的定义,只要把三角形向右平移2格,即可与长方形组成轴对称图形,据此即可画出它们的对称轴;
(3)以点O为旋转中心,把长方形的另外三个顶点分别绕点O,旋转90度,再把它们依次连接起来,即可得出旋转后的长方形,再根据数对表示位置的方法即可标出点D旋转后的数对位置;
(4)三角形的底与高原来都是4,按1:2缩小后的底与高分别是4÷2=2,据此即可画出缩小后的三角形,再根据三角形的面积公式分别计算出缩小前后的面积比,即可解答问题.
(2)根据轴对称图形的定义,只要把三角形向右平移2格,即可与长方形组成轴对称图形,据此即可画出它们的对称轴;
(3)以点O为旋转中心,把长方形的另外三个顶点分别绕点O,旋转90度,再把它们依次连接起来,即可得出旋转后的长方形,再根据数对表示位置的方法即可标出点D旋转后的数对位置;
(4)三角形的底与高原来都是4,按1:2缩小后的底与高分别是4÷2=2,据此即可画出缩小后的三角形,再根据三角形的面积公式分别计算出缩小前后的面积比,即可解答问题.
解答:解:根据题干分析画图如下:
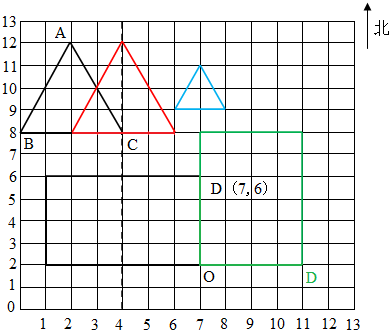
(1)通过测量,点A在点B的东偏北65度,因为这个三角形是等腰三角形,所以∠C=65度.
(3)观察图形可知,点D旋转后的对应位置用数对可表示为(11,2);
(4)(2×2÷2):(4×4÷2)=2:8=1:4,
所以按1:2的比画出这个三角形缩小后的图形,新图形与原来图形的面积比是:1:4.
故答案为:65;65;(11,2);1:4.

(1)通过测量,点A在点B的东偏北65度,因为这个三角形是等腰三角形,所以∠C=65度.
(3)观察图形可知,点D旋转后的对应位置用数对可表示为(11,2);
(4)(2×2÷2):(4×4÷2)=2:8=1:4,
所以按1:2的比画出这个三角形缩小后的图形,新图形与原来图形的面积比是:1:4.
故答案为:65;65;(11,2);1:4.
点评:此题主要考查数对表示位置、方向与距离表示位置的方法以及利用平移、旋转、放大与缩小的方法进行图形变换的方法.

练习册系列答案
相关题目