Question

6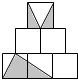．用六个同样大小的正方形拼成下面的图形，其中阴影部分的面积共12平方厘米，你能算出图中空白部分的面积共有多少平方厘米吗？

Answer 1

分析 观察图形可以发现：上面的阴影部分的面积等于小正方形的面积的一半，下面的阴影部分的面积等于两个小正方形的面积的一半，即等于1个小正方形的面积，据此可以得出，整个阴影部分的面积就等于1+$\frac{1}{2}$=$\frac{3}{2}$个小正方形的面积，阴影部分的面积已知，于是用除法计算即可求出小正方形的面积，从而得出整个图形的面积．然后减去阴影部分的面积，就是空白部分的面积．

解答 解：据分析可知：
整个阴影部分的面积就等于1+$\frac{1}{2}$=$\frac{3}{2}$个小正方形的面积，
12÷$\frac{3}{2}$=8（平方厘米）
8×6-12
=48-12
=36（平方厘米）
答：图中空白部分的面积共有36平方厘米．

点评 解答此题的关键是：弄清楚阴影部分的面积和小正方形的面积的关系，计算出每个小正方形的面积，问题即可得解．