题目内容
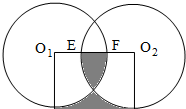 (2011?河西区)如图所示,O1、O2分别是所在圆的圆心.如果两圆半径均为2厘米,且图中两块阴影部分的面积相等,那么EF的长度是
(2011?河西区)如图所示,O1、O2分别是所在圆的圆心.如果两圆半径均为2厘米,且图中两块阴影部分的面积相等,那么EF的长度是0.86
0.86
厘米.分析:根据长方形中,一个空白部分的面积加上其中一个阴影部分的面积等于另一个空白部分面积加上另一个阴影部分的面积可得长方形的面积等于扇形面积的2倍,从而可求长方形的面积,再根据线段之间的和差关系求解即可.
解答:解:因为两个阴影部分的面积相等,所以长方形的面积等于扇形面积的2倍,
而其中一个扇形的面积=
π×22=π(cm2),
故整个长方形的面积=2π(cm2),
故两个圆心连接的线段O1O2=面积÷宽=2π÷2=π(cm),
故EF=2+2-π=4-π=4-3.14=0.86(cm).
答:EF的长度是0.86厘米.
故答案为:0.86.
而其中一个扇形的面积=
| 1 |
| 4 |
故整个长方形的面积=2π(cm2),
故两个圆心连接的线段O1O2=面积÷宽=2π÷2=π(cm),
故EF=2+2-π=4-π=4-3.14=0.86(cm).
答:EF的长度是0.86厘米.
故答案为:0.86.
点评:考查了组合图形的面积,本题难度较大,解题的关键是得到整个长方形的面积.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目