题目内容
 已知等边三角形的周长是360米,甲从A点出发,按顺时针方向前进,每分走30米;乙从C点出发,按顺时针方向以每分55米的速度前进,两人同时出发,几分钟相遇?
已知等边三角形的周长是360米,甲从A点出发,按顺时针方向前进,每分走30米;乙从C点出发,按顺时针方向以每分55米的速度前进,两人同时出发,几分钟相遇?
解:360÷3=120(米),
120÷(55-30),
=120÷25,
=4.8(分钟);
答:4.8分钟相遇.
分析:等边三角形的周长是360米,可得一条边的长度360÷3=120米,由图可知甲从A点、乙从C点,按顺时针方两人同时出发,是追及问题,当两人相遇时,乙比甲多走的路程正好是三角形的一条边长度120米,就根据乙行的路程-甲行的路程=120米,可得路程差÷速度差=相遇时间,即可列式解答.
点评:此题是不同地点同一方向,知道快的追上慢的相遇时所走的路程就是出发时两点的距离,再根据路程差÷速度差=相遇时间即可求出.
120÷(55-30),
=120÷25,
=4.8(分钟);
答:4.8分钟相遇.
分析:等边三角形的周长是360米,可得一条边的长度360÷3=120米,由图可知甲从A点、乙从C点,按顺时针方两人同时出发,是追及问题,当两人相遇时,乙比甲多走的路程正好是三角形的一条边长度120米,就根据乙行的路程-甲行的路程=120米,可得路程差÷速度差=相遇时间,即可列式解答.
点评:此题是不同地点同一方向,知道快的追上慢的相遇时所走的路程就是出发时两点的距离,再根据路程差÷速度差=相遇时间即可求出.

练习册系列答案
相关题目
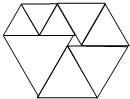 (2013?北京模拟)图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1厘米,这个六边形的周长是多少厘米?
(2013?北京模拟)图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1厘米,这个六边形的周长是多少厘米?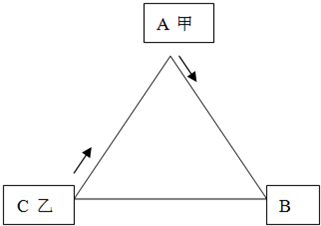 已知等边三角形的周长是360米,甲从A点出发,按顺时针方向前进,每分走30米;乙从C点出发,按顺时针方向以每分55米的速度前进,两人同时出发,几分钟相遇?
已知等边三角形的周长是360米,甲从A点出发,按顺时针方向前进,每分走30米;乙从C点出发,按顺时针方向以每分55米的速度前进,两人同时出发,几分钟相遇?