Question

求下面各图形的面积．（单位：分米）

Answer 1

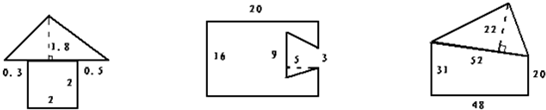
解：根据题干分析可得：
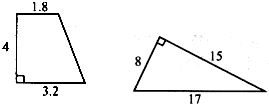
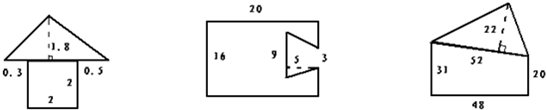
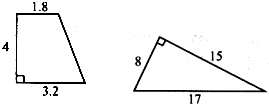
（1）（0.3+2+0.5）×1.8÷2+2×2，
=2.8×0.9+4，
=6.52（平方分米）；
答：这个组合图形的面积是6.52平方分米．
（2）20×16-（3+9）×5÷2，
=320-30，
=290（平方分米）；
答：这个组合图形的面积是290平方分米．
（3）52×22÷2+（20+31）×48÷2，
=572+1224，
=1796（平方分米）；
答：这个组合图形的面积是1796平方分米．
分析：（1）这幅图形的面积是指底为0.3+2+0.5=2.8分米，高为1.8分米的三角形和边长为2分米的正方形的面积之和，利用三角形的面积公式及正方形的面积公式即可解决问题；
（2）此题可以看做是大长方形与空缺处的梯形的面积之差，利用长方形和梯形的面积公式代入数据即可解决问题；
（3）此幅图是三角形和直角梯形的面积之和，利用三角形和梯形的面积公式代入数据即可解决问题．
点评：求组合图形的面积时，一般都要利用分割法或是添补法将其转化成几个规则图形的和或是差的形式，然后利用规则图形的面积公式进行解答．