题目内容
四边形内有10个点,以四边形的4个顶点和这10个点为三角形的顶点,最多能剪出多少个小三角形?
解:在10个点中任取一点A,连接A与四边形的四个顶点,构成4个三角形.再在剩下的9个点中任取一点B.如果B在某个三角形中,那么连接B与B所在的三角形的三个顶点,此时三角形总数增加2个(见左下图).如果B在某两个三角形的公共边上,那么连接B与B所在边相对的顶点,此时三角形总数也是增加2个(见右下图).
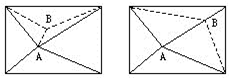
类似地,每增加一个点增加2个三角形.
所以,共可剪出三角形4+2×9=22(个).
分析:首先四边形内,若加入一个点,是4个小三角形,若再加一个,等于在其中一个三角形加一点,与三个顶点连接变成3个,减去原来一个,就是只能增加2个,以后都是这样,当加到10个时,加了9个2个,一共是22个.
点评:此题关键是理解在10个点中任取一点A,连接A与四边形的四个顶点,构成4个三角形,以后每增加一个点就增加2个三角形.

类似地,每增加一个点增加2个三角形.
所以,共可剪出三角形4+2×9=22(个).
分析:首先四边形内,若加入一个点,是4个小三角形,若再加一个,等于在其中一个三角形加一点,与三个顶点连接变成3个,减去原来一个,就是只能增加2个,以后都是这样,当加到10个时,加了9个2个,一共是22个.
点评:此题关键是理解在10个点中任取一点A,连接A与四边形的四个顶点,构成4个三角形,以后每增加一个点就增加2个三角形.

练习册系列答案
相关题目