题目内容
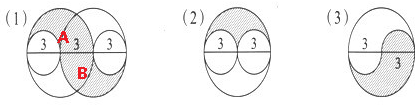
下面三个图形的设计都非常精巧、美丽,寓意深刻.请你先欣赏,再计算出每个图中阴影部分的面积.(图中单位:厘米)


分析:(1)阴影部分分成上下AB两部分计算:这两部分面积都等于大圆面积的一半减去小圆面积的一半,据此求出其中一部分的面积,再乘2即可求出阴影部分的面积;
(2)阴影部分的面积等于大圆面积的一半与一个小圆的面积之差,据此利用圆的面积公式计算即可;
(3)把这部分阴影部分的小半圆旋转到下面的空白处的小半圆处,则可得阴影部分的面积正好等于大半圆的面积,据此计算即可解答.
(2)阴影部分的面积等于大圆面积的一半与一个小圆的面积之差,据此利用圆的面积公式计算即可;
(3)把这部分阴影部分的小半圆旋转到下面的空白处的小半圆处,则可得阴影部分的面积正好等于大半圆的面积,据此计算即可解答.

解答:解:(1)[3.14×32÷2-3.14×(3÷2)2÷2]×2
=[14.13-3.5325]×2
=10.5975×2
=21.195(平方厘米)
答:阴影部分的面积是21.195平方厘米.
(2)3.14×32÷2-3.14×(3÷2)2
=14.13-7.065
=7.065(平方厘米)
答:阴影部分的面积是7.065平方厘米.
(3)3.14×32÷2
=3.14×9÷2
=14.13(平方厘米)
答:阴影部分的面积是14.13平方厘米.
=[14.13-3.5325]×2
=10.5975×2
=21.195(平方厘米)
答:阴影部分的面积是21.195平方厘米.
(2)3.14×32÷2-3.14×(3÷2)2
=14.13-7.065
=7.065(平方厘米)
答:阴影部分的面积是7.065平方厘米.
(3)3.14×32÷2
=3.14×9÷2
=14.13(平方厘米)
答:阴影部分的面积是14.13平方厘米.
点评:此题考查了不规则图形的面积的计算方法,一般都是转化到规则图形中,利用面积公式计算解答.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目