题目内容
【题目】如图，四边形ABCD是平行四边形，BE：EC=1：2，F是DC的中点，三角形ABE的面积是12cm2， 那么三角形ADF的面积是（ ）.
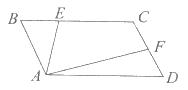
A. 36cm2B. 12cm2C. 24cm2D. 18cm2
【答案】D
【解析】
两个三角形的高相等，对应的底的长度比就是两个三角形的面积比，这样先计算三角形ACE的面积，再确定三角形ACB的面积，然后确定三角形ADF的面积。
如图，连接AC，
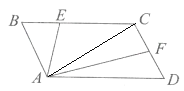
因为BE：EC=1：2，所以三角形ACE的面积是三角形ABE的2倍，三角形ACE的面积：12×2=24（cm）；
三角形ACB的面积：12+24=36（cm）；
三角形ACD的面积与三角形ACB的面积相等，因为F是DC的中点，所以三角形ACF的面积与三角形ADF的面积相等，三角形ADF的面积：36÷2=18（cm）。
故答案为：D。
练习册系列答案
相关题目