Question

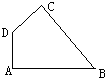[巧妙拼接]．如图，在四边形ABCD中，∠A=∠C=90°，∠B=45°，AB=12厘米，DC=4厘米，四边形ABCD的面积是多少平方厘米？

Answer 1

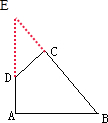
解：延长AD，延长BC，相交于E点，得到两个等腰直角三角形△ABE和△CDE，
由等腰直角三角形的性质得：
CE=AB=12厘米，
CE=CD=4厘米，
那么四边形ABCD的面积是：
12×12÷2-4×4÷2，
=72-8，
=64（平方厘米）；
答：四边形ABCD的面积是64平方厘米．
分析：如上图所示，延长AD，延长BC，相交于E点．△ABE是等腰直角三角形，AE=AB=12厘米，则可以求出△ABE的面积；∠B=∠E=45度，所以△CDE是等腰直角三角形，CE=CD=4厘米，则可以求出△CDE的面积；那么四边形ABCD的面积是两个三角形的面积之差．

点评：此题考查了图形的拆拼（切拼）和组合图形的面积，做延长线，找到交点，组成新图形，是解决此题的关键．