题目内容
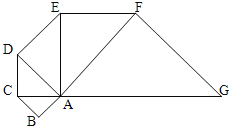
【题目】如图,以等腰直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以等腰直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角ADE,…,以此类推直到第五个等腰直角三角形AFG.已知,这五个等腰直角三角形的面积和为15.5,求原来等腰直角三角形ABC的直角边的长.
【答案】原来等腰直角三角形ABC的直角边的长为1.
【解析】
试题分析:假设AB的长为x,那么根据三角形的面积公式可知△ABC的面积就是![]() x2;AC2=2x2,等腰直角三角形ACD的面积=
x2;AC2=2x2,等腰直角三角形ACD的面积=![]() AC×CD=
AC×CD=![]() AC2=x2;AD2=2AC2=4x2,等腰直角三角ADE的面积=
AC2=x2;AD2=2AC2=4x2,等腰直角三角ADE的面积=![]() AD×DE=
AD×DE=![]() AD2=2x2,以此类推,等腰直角三角形AEF的面积=4x2,等腰直角三角形AFG的面积=8x2,根据这五个等腰直角三角形的面积和为15.5列出方程,即可求出原来等腰直角三角形ABC的直角边的长.
AD2=2x2,以此类推,等腰直角三角形AEF的面积=4x2,等腰直角三角形AFG的面积=8x2,根据这五个等腰直角三角形的面积和为15.5列出方程,即可求出原来等腰直角三角形ABC的直角边的长.
解:设AB的长为x,
![]() x2+x2+2x2+4x2+8x2=15.5
x2+x2+2x2+4x2+8x2=15.5
15.5x2=15.5
x2=1
x=1
或x=﹣1(不合题意,舍去),
答:原来等腰直角三角形ABC的直角边的长为1.

练习册系列答案
相关题目