题目内容
 如图,大圆半径为6厘米,则其阴影部分的面积是多少?(保留π)
如图,大圆半径为6厘米,则其阴影部分的面积是多少?(保留π)分析:每个小圆中有两个空白椭圆形,将它们平均分成两部分,则圆中的阴影部分可补到空白部分,则每个小圆中的阴影部分可割补成一个阴影小正方形,4个阴影小正方形组成了一个大阴影正方形,大正方形的对角线就是大圆的直径,正方形的面积=对角线×对角线÷2,据此解答.


解答:解:阴影部分的面积:
(6×2)×(6×2)÷2,
=12×12÷2,
=144÷2,
=72(cm2).
答:阴影部分的面积是72平方厘米.
(6×2)×(6×2)÷2,
=12×12÷2,
=144÷2,
=72(cm2).
答:阴影部分的面积是72平方厘米.
点评:本题的关键是把不规则阴影部分的面积通过分合割补的方法转化为一个正方形的面积进行求解.

练习册系列答案
相关题目
 如图,大圆半径为2cm,那么图中阴影部分的周长为
如图,大圆半径为2cm,那么图中阴影部分的周长为 如图,大圆半径R=8厘米,小圆的半径r=4厘米.求阴影部分的面积.
如图,大圆半径R=8厘米,小圆的半径r=4厘米.求阴影部分的面积.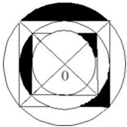 如图,大圆半径R=8厘米,小圆的半径r=4厘米.求阴影部分的面积.
如图,大圆半径R=8厘米,小圆的半径r=4厘米.求阴影部分的面积.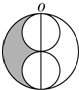 如图,大圆半径为2cm,那么图中阴影部分的周长为________cm,面积是________cm2.
如图,大圆半径为2cm,那么图中阴影部分的周长为________cm,面积是________cm2.