题目内容
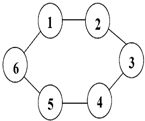 如图,一只蚂蚱站在1号位置上,第1次跳1步,站在2号位置上;第2次跳2步,站在4号位置上;第3次跳3步,站在1号位置上…第n次跳n步.当蚂蚱沿顺时针方向跳100次时,到达________号位置上.
如图,一只蚂蚱站在1号位置上,第1次跳1步,站在2号位置上;第2次跳2步,站在4号位置上;第3次跳3步,站在1号位置上…第n次跳n步.当蚂蚱沿顺时针方向跳100次时,到达________号位置上.
4
分析:这是一道数列求和的问题,根据高斯定理,我们可以很容易地求出蚂蚱跳了100次时,共跳出了多少步,(1+100)×100÷2=5050(步).因为是在圆周上转圈跳动,所以,接下来就变成了周期性问题了(跳6步为一周期).5050÷6=841…4,,所以,当跳了100次时,到达的位置是4号位置.
解答:①蚂蚱跳了100次时,共跳出
(1+100)×100÷2=5050(步).
②5050÷6=841…4,
所以,当跳了100次时,到达的位置是4号位置.
故答案为:4.
点评:此题考查了高斯求和公式的运用,以及探索算术中的规律的能力.
分析:这是一道数列求和的问题,根据高斯定理,我们可以很容易地求出蚂蚱跳了100次时,共跳出了多少步,(1+100)×100÷2=5050(步).因为是在圆周上转圈跳动,所以,接下来就变成了周期性问题了(跳6步为一周期).5050÷6=841…4,,所以,当跳了100次时,到达的位置是4号位置.
解答:①蚂蚱跳了100次时,共跳出
(1+100)×100÷2=5050(步).
②5050÷6=841…4,
所以,当跳了100次时,到达的位置是4号位置.
故答案为:4.
点评:此题考查了高斯求和公式的运用,以及探索算术中的规律的能力.

练习册系列答案
相关题目
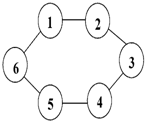 如图,一只蚂蚱站在1号位置上,第1次跳1步,站在2号位置上;第2次跳2步,站在4号位置上;第3次跳3步,站在1号位置上…第n次跳n步.当蚂蚱沿顺时针方向跳100次时,到达
如图,一只蚂蚱站在1号位置上,第1次跳1步,站在2号位置上;第2次跳2步,站在4号位置上;第3次跳3步,站在1号位置上…第n次跳n步.当蚂蚱沿顺时针方向跳100次时,到达