题目内容
16.简算:$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$.分析 $\frac{1}{2}$=$\frac{1}{1×2}$=1$-\frac{1}{2}$,$\frac{1}{6}$=$\frac{1}{2×3}$=$\frac{1}{2}$$-\frac{1}{3}$…$\frac{1}{56}$=$\frac{1}{7×8}$=$\frac{1}{7}-\frac{1}{8}$,依次按照$\frac{1}{n(n-1)}$=$\frac{1}{n}$-$\frac{1}{n-1}$展开,前后加减相同分数抵消,即可得解.
解答 解:$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$
=1-$\frac{1}{2}$$+\frac{1}{2}-\frac{1}{3}$$+\frac{1}{3}-\frac{1}{4}$+…$\frac{1}{7}-\frac{1}{8}$
=1-$\frac{1}{8}$
=$\frac{7}{8}$
点评 灵活应用分数$\frac{1}{n(n-1)}$=$\frac{1}{n}$-$\frac{1}{n-1}$展开是解决此题的关键.

练习册系列答案
相关题目
4.如果a比b多$\frac{2}{7}$,则a与b的比是( )
| A. | 7:9 | B. | 9:7 | C. | 7:5 | D. | 5:7 |
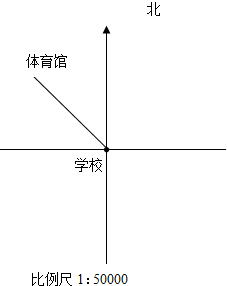 如图:
如图: