题目内容
【题目】如图,三棱锥![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() ,
, ![]() .
.
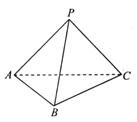
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)通过证明线面垂直,由面面垂直的判定定理,得出面面垂直;(2)先作出二面角![]() 的平面角,再证明,再由余弦定理求出二面角的余弦值。
的平面角,再证明,再由余弦定理求出二面角的余弦值。
试题解析:(1)取AC的中点O,连接BO,PO.
因为ABC是边长为2的正三角形,所以BO⊥AC,BO=![]() .
.
因为PA⊥PC,所以PO=![]() .
.
因为PB=2,所以OP2+OB2==PB2,所以PO⊥OB.
因为AC,OP为相交直线,所以BO⊥平面PAC.
又OB平面ABC,所以平面PAB⊥平面ABC.
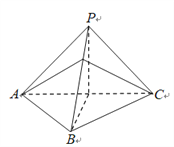
(2)因为PA=PB,BA=BC,所以![]() ≌
≌![]() .
.
过点A作![]() 于D,则
于D,则![]() .
.
所以![]() 为所求二面角A﹣PB﹣C 的平面角.
为所求二面角A﹣PB﹣C 的平面角.
因为PA=PC,PA⊥PC,AC=2,所以![]() .
.
在![]() 中,求得
中,求得![]() ,同理
,同理![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() .
.
所以,二面角A﹣PB﹣C的余弦值为![]() .
.

练习册系列答案
相关题目