题目内容
8.如图有一直角三角形,直角边分别为6cm和8cm,在直角三角形内作一个最大正方形,求正方形的面积.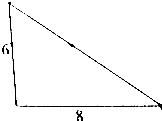
分析 如下图所示:在直角三角形ABC内作一个最大正方形DBFE,设正方形的边长为xcm,则DE=DB=xcm,AD=6-x(cm),由DE∥BC,可得三角形ADE∽三角形ABC,则有$\frac{AD}{AB}$=$\frac{DE}{BC}$,即$\frac{6-x}{6}$=$\frac{x}{8}$,解得x=$\frac{24}{7}$;再利用正方形的面积公式可求出正方形的面积.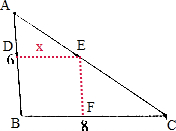
解答 解:在直角三角形ABC内作一个最大正方形DBFE,如上图所示,
设正方形的边长为xcm,则DE=DB=xcm,AD=6-x(cm),
因为DE∥BC,
所以三角形ADE∽三角形ABC,
所以$\frac{AD}{AB}$=$\frac{DE}{BC}$,
即$\frac{6-x}{6}$=$\frac{x}{8}$,
解得x=$\frac{24}{7}$;
所以正方形的边长为$\frac{24}{7}$cm,
面积为:$\frac{24}{7}$×$\frac{24}{7}$=$\frac{576}{49}$(cm2).
答:正方形的面积是$\frac{576}{49}$cm2.
点评 本题解决的关键是求出直角三角形内最大正方形的边长,利用相似三角形的性质列出方程解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
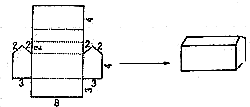 (1)将下面的图形,按照虚线折叠成一个封闭的立体图形,它的形状像什么?(单位:cm)
(1)将下面的图形,按照虚线折叠成一个封闭的立体图形,它的形状像什么?(单位:cm) 在长方形ABCD-EFGH中,已知从点F出发的三条棱EF、BF、FG的长度之比为3:4:3,该长方体的棱长的总和为80cm,求:
在长方形ABCD-EFGH中,已知从点F出发的三条棱EF、BF、FG的长度之比为3:4:3,该长方体的棱长的总和为80cm,求: