Question

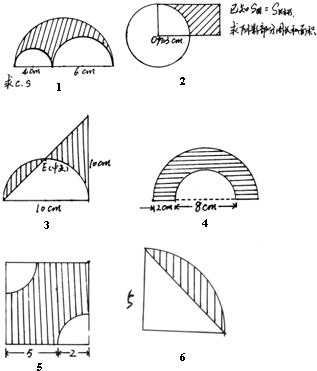第1、2题求阴影部分周长和面积，第3-6题只求阴影部分面积．

Answer 1

解：（1）阴影部分的周长：
3.14×（4+6+4+6）÷2，
=3.14×20÷2，
=31.4（厘米）；
阴影部分的面积：
[3.14×（10÷2）²-3.14×（4÷2）²-3.14×（6÷2）²]÷2，
=[3.14×25-3.14×4-3.14×9]÷2，
=[3.14×（25-4-9）]÷2，
=[3.14×12]÷2，
=37.68÷2，
=18.84（平方厘米）；

（2）阴影部分的周长：
3.14×3×2×+3×2×2，
=4.71+12，
=16.71（厘米）；
阴影部分的面积：
3×2×3-3.14×3²×，
=18-3.14×9×，
=18-7.065，
=10.935（平方厘米）；

（3）阴影部分的面积：
10×10÷2÷2=25（平方厘米）；

（4）阴影部分的面积：
3.14×（8÷2+2）²÷2-3.14×（8÷2）²÷2，
=3.14×36÷2-3.14×16÷2，
=56.52-25.12，
=31.4（平方厘米）；

（5）（5+2）×（5+2）-3.14×2²×，
=7×7-3.14×4×，
=49-6.28，
=42.72（平方厘米）；

（6）阴影部分的面积：
3.14×5²×-5×5÷2，
=3.14×25×-12.5，
=19.625-12.5，
=7.125（平方厘米）．
分析：（1）阴影部分的周长等于直径4厘米，直径6厘米，直径（4+6）厘米，3个圆的周长的一半，阴影部分的面积用大半圆的面积减去2个小半圆的面积．
（2）阴影部分的周长等于半径3厘米的圆的周长的加上长方形的两条长边（因为长是宽的2倍），阴影部分的面积用 长方形的面积减去半径3厘米的圆面积的．
（3）通过旋转把两部分阴影拼在一起正好是三角形面积的一半，根据三角形的面积公式解答．
（4）根据环形面积的计算方法求环形的面积再除以2即可．
（5）用正方形的面积减去两个半径是2厘米，圆心角是90°的扇形面积．
（6）用半径5厘米圆心角是90°的扇形面积减去三角形的面积．
点评：此题主要考查求组合图形的周长和面积，解答关键是明确周长和面积的意义，认真分析图形是由几部分组成，然后再根据相应的公式进行解答．