题目内容
【题目】如图，正方形ABCD的边长为4厘米，AE=2BE，求三角形CDF的面积．
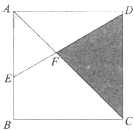
【答案】4.8平方厘米
【解析】
试题分析：由题意可知：三角形AEF与三角形ADF等高不等底，则它们的面积比就等于底的比，因为AE=2BE，AB=AD，所以AE：AB=AE：AD=AE：（AE+BE）=2：3，则三角形AEF和三角形ADF面积比=EF：DF=AE：AD=2：3，进而可以求出三角形ADF的面积：三角形AED的面积=3：5，所以三角形ADF的面积等于三角形AED的面积的
，然后用三角形ACD的面积减去三角形ADF的面积就是三角形CDF的面积．
解：由题意可知AE=2BE，AB=AD，
则AE：AB=AE：AD=AE：（AE+BE）=2：3，
所以三角形AEF和三角形ADF面积比=EF：DF=AE：AD=2：3；
三角形ADF的面积：三角形AED的面积=3：（2+3）=3：5；
三角形AED的面积为4×
×4÷2=
（平方厘米）
所以三角形ADF的面积为×=
（平方厘米）
三角形CDF的面积为4×4÷2
=8=4.8（平方厘米）；
答：三角形CDF的面积是4.8平方厘米
练习册系列答案
相关题目
【题目】根据统计表完成下面各题。
种类 | 客车 | 货车 | 面包车 | 小轿车 |
辆数（辆） | 20 | 15 | 35 | 40 |
（1）小轿车比客车多多少辆？
（2）什么车最少，什么车最多？
（3）货车和面包车相差多少辆？
（4）客车和货车的总辆数和什么车同样多？
（5）这四种车一共有多少辆？
