题目内容
【题目】如图，在三角形ABC中，点D、E、F分别为AB、BC、CA延长线的点，且
=2；
=3；
=4，三角形ABC的面积为1，则三角形DEF的面积为 ．
【答案】20.5．
【解析】
试题分析：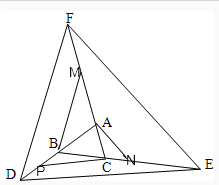
过点B作线段DE的平行线交线段AF与点M，过点A作线段EF的平行线交线段CE与点N，过点C作线段DE的平行线交线段DB与点P，因为
=2；
=3；
=4，所以MA：AC=1.5：1，CN：BC=1：2，PB：AB=1：2，根据等高的三角形的面积之比等于底的比，即可求得三角形AMB的面积=2三角形ABC的面积=2×1=2，三角形ANC的面积=三角形ABC面积的一半=1÷2=0.5，三角形CBP的面积=三角形ABC面积的一半=1÷2=0.5，再根据相似三角形面积的比等于相似比的平方求得：三角形AMB的面积：三角形ADF的面积=（1：2）2，得出三角形ADF的面积=8，同理可得：三角形CEF的面积=16×0.5=8，三角形DBE的面积=9×0.5=4.5，故此三角形AEF的面积=8+8+4.5=20.5，据此解答即可．
解：如图：
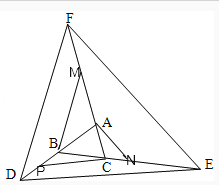
过点B作线段DE的平行线交线段AF与点M
过点A作线段EF的平行线交线段CE与点N
过点C作线段DE的平行线交线段DB与点P
因为：
且=2；=3；=4
所以：
M：DF=AB：AD=1：2
AN：EF=CA：CF=1：4
PC：DB=BC：BE=1：3
MA：AC=1.5：1，CN：BC=1：2，PB：AB=1：2
根据等高的三角形面积之比等于它们底的比，所以：
三角形AMB的面积=2三角形ABC的面积=2×1=2
三角形ANC的面积=三角形ABC面积的一半=1÷2=0.5
三角形CBP的面积=三角形ABC面积的一半=1÷2=0.5
所以：
三角形AMB的面积：三角形ADF的面积=（1：2）2
三角形ADF的面积=8
同理可得：
三角形CEF的面积=16×0.5=8
三角形DBE的面积=9×0.5=4.5
而：
三角形AEF的面积
=三角形ADF的面积+三角形CEF的面积+三角形DBE的面积
=8+8+4.5
=20.5
答：三角形DEF的面积为20.5
