题目内容
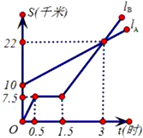 如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,B出发时与A相距10千米;B骑了一段路后,自行车发生故障,进行修理;最后从起点出发后3小时与A相遇.
如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,B出发时与A相距10千米;B骑了一段路后,自行车发生故障,进行修理;最后从起点出发后3小时与A相遇.
(1)B修车用时______.
(2)A和B的速度各是多少?
(3)假设B的自行车没有发生故障,保持出发时的速度前进,多久能和A相遇?
解:如图,

(1)1.5-0.5=1(小时)
答:B修车用的时间是1小时;
(2)(22-10)÷3
=12÷3
=4(千米/小时),
7.5÷0.5
=15(千米/小时),
答:A和B的速度分别是4千米/小时、15千米/小时;
(3)设B的自行车没有发生故障,保持出发时的速度前进,x小时能和A相遇,
15x=4x+10
15x-4x=4x-4x+10,
11x=10,
x= ;
;
答:假设B的自行车没有发生故障,保持出发时的速度前进, 能和A相遇;
能和A相遇;
故答案为:1小时.
分析:(1)从复式折线统计图中可以看出:B出发后0.5小时自行车发生故障,到出发后1.5小时修好,用修好车的时刻减去车发生故障的时刻就是修车用的时间.
(2)从图中可以看出,A出发3小时后所走的路程是(22-10)千米,B出发0.5小时所走的路程是7.5千米,根据速度= 即可分别求出A、B的速度.
即可分别求出A、B的速度.
(3)A和B相遇,A比B少走10千米,根据根据“路程=速度×时间”、“A走的路程+10=B走的路程”可列方程解答.
点评:本题是考查从复式折线统计图中获取信息,并根据所获取的信息进行行程问题的计算.

(1)1.5-0.5=1(小时)
答:B修车用的时间是1小时;
(2)(22-10)÷3
=12÷3
=4(千米/小时),
7.5÷0.5
=15(千米/小时),
答:A和B的速度分别是4千米/小时、15千米/小时;
(3)设B的自行车没有发生故障,保持出发时的速度前进,x小时能和A相遇,
15x=4x+10
15x-4x=4x-4x+10,
11x=10,
x=
 ;
;答:假设B的自行车没有发生故障,保持出发时的速度前进,
 能和A相遇;
能和A相遇;故答案为:1小时.
分析:(1)从复式折线统计图中可以看出:B出发后0.5小时自行车发生故障,到出发后1.5小时修好,用修好车的时刻减去车发生故障的时刻就是修车用的时间.
(2)从图中可以看出,A出发3小时后所走的路程是(22-10)千米,B出发0.5小时所走的路程是7.5千米,根据速度=
 即可分别求出A、B的速度.
即可分别求出A、B的速度.(3)A和B相遇,A比B少走10千米,根据根据“路程=速度×时间”、“A走的路程+10=B走的路程”可列方程解答.
点评:本题是考查从复式折线统计图中获取信息,并根据所获取的信息进行行程问题的计算.

练习册系列答案
相关题目

 如图,已知两边分别是6厘米和10厘米,其中一条底上的高是8厘米,这个平行四边形的面积是
如图,已知两边分别是6厘米和10厘米,其中一条底上的高是8厘米,这个平行四边形的面积是 如图,B、C分别是正方形边上的中点,己知正方形的周长是80厘米.阴影部分的面积是
如图,B、C分别是正方形边上的中点,己知正方形的周长是80厘米.阴影部分的面积是 如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,B出发时与A相距10千米;B骑了一段路后,自行车发生故障,进行修理;最后从起点出发后3小时与A相遇.
如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,B出发时与A相距10千米;B骑了一段路后,自行车发生故障,进行修理;最后从起点出发后3小时与A相遇.