Question

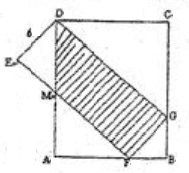两个长方形如图摆放，M为AD的中点，∠MDG=45°，阴影部分的面积=________．

Answer 1

90
分析：由图易得：DE=EM=GF=6，M为AD中点，则三角形MAF为等腰直角三角形，于是有MF=12，DG=MF+EM=18，则阴影部分的面积可以利用梯形的面积公式求解．
解答：由题意可得：DE=EM=GF=6，M为AD中点，
则三角形MAF为等腰直角三角形，
于是有MF=12，DG=MF+EM=18，
阴影部分的面积为：（12+18）×6÷2，
=30×6÷2，
=180÷2，
=90；
答：阴影部分的面积是90．
故答案为：90．
点评：解答此题的关键是求出阴影部分的上底和下底的值，进而利用梯形的面积公式求解．