题目内容
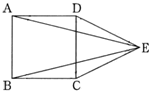 图中四边形ABCD是正方形、三角形CDE是等边三角形,那么,∠AEB=________度.
图中四边形ABCD是正方形、三角形CDE是等边三角形,那么,∠AEB=________度.
30
分析:正方形、正三角形各边长相等,故DA=DE,CB=CE,∴∠DAE=∠DEA,∠CBE=∠CEB,∵∠ADE-90°+60°=150°,∴∠DEA=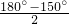 =15°,同理可证∠CEB=15°,即可求∠AEB的大小.
=15°,同理可证∠CEB=15°,即可求∠AEB的大小.
解答:正方形、正三角形各边长相等,故DA=DE,
∴∠DAE=∠DEA,
又∵∠ADE-90°+60°=150°,
∴∠DEA=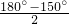 =15°,
=15°,
同理可证∠CEB=15°,
∴∠AEB=∠DEC-∠DEA-∠CEB=30°.
故答案为:30.
点评:本题考查了正方形各边长相等的性质,正三角形各内角为60°,各边长相等的性质,等腰三角形的性质,本题中正确计算∠DEA和∠CEB是解题的关键.
分析:正方形、正三角形各边长相等,故DA=DE,CB=CE,∴∠DAE=∠DEA,∠CBE=∠CEB,∵∠ADE-90°+60°=150°,∴∠DEA=
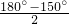 =15°,同理可证∠CEB=15°,即可求∠AEB的大小.
=15°,同理可证∠CEB=15°,即可求∠AEB的大小.解答:正方形、正三角形各边长相等,故DA=DE,
∴∠DAE=∠DEA,
又∵∠ADE-90°+60°=150°,
∴∠DEA=
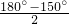 =15°,
=15°,同理可证∠CEB=15°,
∴∠AEB=∠DEC-∠DEA-∠CEB=30°.
故答案为:30.
点评:本题考查了正方形各边长相等的性质,正三角形各内角为60°,各边长相等的性质,等腰三角形的性质,本题中正确计算∠DEA和∠CEB是解题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 在图中,ABCD是长方形,三条线段的长度如图所示,M是线段DE的中点,求四边形ABMD(阴影部分)的面积(单位:厘米).
在图中,ABCD是长方形,三条线段的长度如图所示,M是线段DE的中点,求四边形ABMD(阴影部分)的面积(单位:厘米).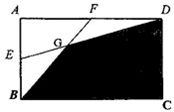 如图中,ABCD是长方形,E,F分别是AB,DA的中点,G是BF和DE的交点,四边形BCDG的面积是40平方厘米,那么ABCD的面积是
如图中,ABCD是长方形,E,F分别是AB,DA的中点,G是BF和DE的交点,四边形BCDG的面积是40平方厘米,那么ABCD的面积是
 图中四边形ABCD是正方形、三角形CDE是等边三角形,那么,∠AEB=
图中四边形ABCD是正方形、三角形CDE是等边三角形,那么,∠AEB=