题目内容
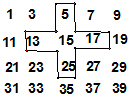 将连续的奇数1,3,5,7,9…,排成如下的数表:
将连续的奇数1,3,5,7,9…,排成如下的数表:(1)十字框中的五个数的平均数与15有什么关系?
(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.
分析:(1)先算出十字框中的五个数的平均数,再找与15的关系;
(2)根据(1)和十字框上下左右平移,可框住另外的五个数的规律是十字框中的五个数的平均数就是中间的数,结合表中数的位置,即可做出判断.
(2)根据(1)和十字框上下左右平移,可框住另外的五个数的规律是十字框中的五个数的平均数就是中间的数,结合表中数的位置,即可做出判断.
解答:解:(1)(13+15+17+5+25)÷5,
=75÷5,
=15;
所以十字框中的五个数的平均数就是15即十字框中的五个数的平均数就是中间的数;
(2)315÷5=63;
因为十字框中的五个数的中间数是63,题干的数阵中没有63.
所以不能;
答:(1)十字框中的五个数的平均数与15相等;
(2)不能,题干的数阵中没有63.
=75÷5,
=15;
所以十字框中的五个数的平均数就是15即十字框中的五个数的平均数就是中间的数;
(2)315÷5=63;
因为十字框中的五个数的中间数是63,题干的数阵中没有63.
所以不能;
答:(1)十字框中的五个数的平均数与15相等;
(2)不能,题干的数阵中没有63.
点评:解答此题的关键是,根据所给的框法,及表中数的特点,即可找出它们之间的规律,再根据规律作答即可.

练习册系列答案
相关题目

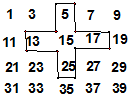 将连续的奇数1,3,5,7,9…,排成如下的数表:
将连续的奇数1,3,5,7,9…,排成如下的数表: