Question

右图四一个三角形网格，由16个小的等边三角形构成．网格中由3个相邻的小三角形构成的图形称为“3-梯形”．如果在每个小三角形内填上数字1-9中的一个，那么能否给出一种填法，使得任意两个“3-梯形”中的3个数之和均不相同？如果能，请举出一例；如果不能，请说明理由．

Answer 1

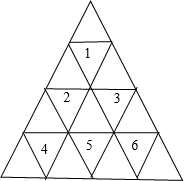
分析：如图：图中和标有数字序号的6个三角形，每个都和它相邻的两个三角形组成三个“3-梯形”，这种“3-梯形”有18个；另外由图中标有数学序号的某两个三角形及它们周围的某个三角形也能组成“3-梯形”，这种“3-梯形”有9个，故一共有27个“3-梯形”；而每个“3-梯形”中的数字之和，最小是三个三角形内都填数字1，和为3，最大是三个三角形内都填数字9，和是27，一共有25个不同结果；因为，27个“3-梯形”中的结果只有25个，至少存在两个“3-梯形”和是相同的；据此解答即可．

解答：解：由分析可知，共有“3-梯形”：18+9=27（个），
而每个“3-梯形”中的数字之和，最小是三个三角形内都填数字1，和为3；
最大是三个三角形内都填数字9，和是27；由3～27，一共有25个不同结果；
因为，27个“3-梯形”中的结果只有25个，至少存在两个“3-梯形”和是相同的，
所以没有一种填法使得任意两个“3-梯形”中的3个数之和均不相同．

点评：根据题意，进行认真分析，得出共有“3-梯形”的个数和“3-梯形”中的3个数之和不同结果的个数，是解答此题的关键．