题目内容
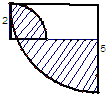
 如图所示,长方形的长是8m,宽是6m,A和B是宽的中点,求长方形内阴影部分的面积.
如图所示,长方形的长是8m,宽是6m,A和B是宽的中点,求长方形内阴影部分的面积.分析:图中阴影部分是4个三角形,设四个小三角形的底边分别是a、b、c、d,则a+b+c+d=AB=8;因为宽是6,A和B是宽的中点,所以这些小三角形的高都相等是6÷2=3,由此根据三角形的面积公式即可解答.
解答:解:设四个小三角形的底边分别是a、b、c、d,则a+b+c+d=8(m);
因为宽是6,A和B是宽的中点,所以这些小三角形的高都是6÷2=3(m),
所以阴影部分的面积是:
×a×3+
×b×3+
×c×3+
×d×3,
=
(a+b+c+d)×3,
=
×8×3,
=12(m2).
答:长方形内阴影部分的面积是12m2.
因为宽是6,A和B是宽的中点,所以这些小三角形的高都是6÷2=3(m),
所以阴影部分的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=12(m2).
答:长方形内阴影部分的面积是12m2.
点评:本题考查组合图形的面积,不规则图形的面积一般都是转化到规则图形中,利用规则图形的面积公式进行计算.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图所示,长方形的长是a厘米,宽是b厘米,剪下最大的正方形,剩下的面积是____平方厘米.( )
如图所示,长方形的长是a厘米,宽是b厘米,剪下最大的正方形,剩下的面积是____平方厘米.( )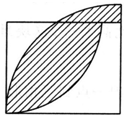 如图所示,长方形的长是6厘米,宽是5厘米,求阴影部分的面积.
如图所示,长方形的长是6厘米,宽是5厘米,求阴影部分的面积.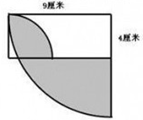 如图所示,长方形的长为9厘米,宽为4厘米,则阴影部分面积为
如图所示,长方形的长为9厘米,宽为4厘米,则阴影部分面积为