题目内容
用数对表示A、B、C、D、E的位置．A（3，2）、B（4，6）、C（5，8）、D（7，6）、E（8，2）
（1）依次连接A、B、C、D、E和A．
（2）求出围成图形的面积．（每小格1cm）
解：（1）根据数对表示位置的方法，在平面图中标出点A、B、C、D、E，并依次连接起来得出一个封闭的不规则图形如图所示；
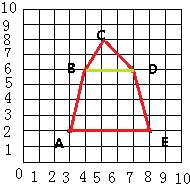
（2）连接BD，则把这个不规则的图形分成了两部分：底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米，高是4厘米的梯形，则这个图形的面积是：
3×2÷2+（3+5）×4÷2，
=3+16，
=19（平方厘米），
答：这个图形的面积是19平方厘米．
分析：（1）数对表示位置的方法是：第一个数字表示列，第二个数字表示行，由此即可在平面图中标出点A、B、C、D、E，并依次连接起来得出一个封闭的不规则图形；
（2）连接BD，则把这个不规则的图形分成了两部分：底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米，高是4厘米的梯形，由此利用三角形和图形的面积公式即可解答．
点评：此题考查了数对表示位置的方法和根据方格图，利用三角形和梯形的面积公式求组合图形的面积的灵活应用．
（2）连接BD，则把这个不规则的图形分成了两部分：底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米，高是4厘米的梯形，则这个图形的面积是：
3×2÷2+（3+5）×4÷2，
=3+16，
=19（平方厘米），
答：这个图形的面积是19平方厘米．
分析：（1）数对表示位置的方法是：第一个数字表示列，第二个数字表示行，由此即可在平面图中标出点A、B、C、D、E，并依次连接起来得出一个封闭的不规则图形；
（2）连接BD，则把这个不规则的图形分成了两部分：底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米，高是4厘米的梯形，由此利用三角形和图形的面积公式即可解答．
点评：此题考查了数对表示位置的方法和根据方格图，利用三角形和梯形的面积公式求组合图形的面积的灵活应用．
练习册系列答案
相关题目
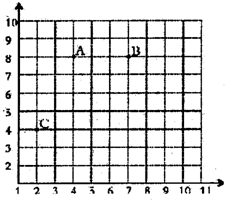的位置．
如图是一个动物园的景点分布图．
（1）用数对表示A、B、C、D的位置．
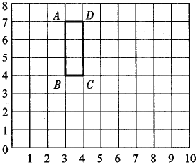看图回答问题．
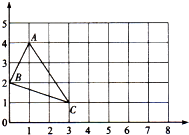看看想想．