题目内容
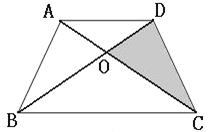
【题目】如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
【答案】![]() 平方厘米
平方厘米
【解析】
试题分析:根据三角形ABC的面积为5平方厘米,BC=5厘米,可以求出三角形ABC的高,即三角形ADC的高,由此即可求出三角形ACD的面积,再根据三角形AOD与三角形BOC相似,得出对应边的比等于对应高的比,求出三角形AOD的高,进而求出三角形AOD的面积,继而求出阴影部分的面积.
解:ABC高是:5×2÷5=2(厘米),
ACD面积是:2×2÷2=2(平方厘米),
因为三角形AOD与三角形BOC相似,
设三角形AOD的高为x厘米,则三角形BOC的高为2﹣x厘米,
所以x:(2﹣x)=2:5,
5x=4﹣2x,
7x=4,
x=![]() ,
,
三角形AOD的面积是:2×![]() ÷2=
÷2=![]() (平方厘米),
(平方厘米),
三角形COD面积是:2﹣![]() =
=![]() (平方厘米),
(平方厘米),
答:阴影部分的面积是![]() 平方厘米.
平方厘米.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目