题目内容
 40根长度相同的火柴棍摆成如图,如果将每根火柴棍看作长度为1的线段,那么其中可以数出30个正方形来.拿走5根火柴棍后,A,B,C,D,E五人分别作了如下的判断:
40根长度相同的火柴棍摆成如图,如果将每根火柴棍看作长度为1的线段,那么其中可以数出30个正方形来.拿走5根火柴棍后,A,B,C,D,E五人分别作了如下的判断:A:“1×1的正方形还剩下5个.”
B:“2×2的正方形还剩下3个.”
C:“3×3的正方形全部保留下来了.”
D:“拿走的火柴棍所在直线各不相同.”
E:“拿走的火柴棍中有4根在同一直线上.”
已知这5人中恰有2人的判断错了,那么剩下的图形中还能数出
14
14
个正方形.分析:根据A、B、C、D、E五个人说的话,结合图形特征进行分析,每拿走1根火柴棍,最多减少2个1×1小正方形,拿5根最多减少10个1×1正方形,所以1×1的正方形至少还有6个,A必错;又因为D、E说的内容相矛盾,必定有一个说错,那么B、C说的都是正确的,据此展开推理即可解答问题.
解答:解:(1)每拿走1根火柴棍,最多减少2个1×1小正方形,拿5根最多减少10个1×1正方形,所以1×1的正方形至少还有6个,A必错;
(2)显然D、E矛盾,必有1错,故B、C都对;
(3)由于C正确,画出组成3×3的火柴,发现只可去掉第三行和第三列的所有火柴,因此D错误;
(4)拿走同一直线的4根火柴(如图),还需要在第三列取走一根.由于2×2的正方形有三个,因此只能取走第三列的第一根.
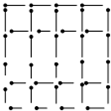
(5)正方形:1×1的6个,2×2的3个.3×3的4个,4×4的1个,共14个.
答:剩下的图形中还能数出 14个正方形.
故答案为:14.
(2)显然D、E矛盾,必有1错,故B、C都对;
(3)由于C正确,画出组成3×3的火柴,发现只可去掉第三行和第三列的所有火柴,因此D错误;
(4)拿走同一直线的4根火柴(如图),还需要在第三列取走一根.由于2×2的正方形有三个,因此只能取走第三列的第一根.

(5)正方形:1×1的6个,2×2的3个.3×3的4个,4×4的1个,共14个.
答:剩下的图形中还能数出 14个正方形.
故答案为:14.
点评:解答此题的关键是根据题干,明确A必错,且D、E矛盾,必有1错,故B、C都对,据此展开推理即可解答问题,难度较大.

练习册系列答案
相关题目