题目内容
 用一些棱长是1的小正方体码堆放成一个立体图,从上向下看这个立体图形,从正面看这个立体图形,所得图形如图所示,则这个立体图形的表面积最多是________.
用一些棱长是1的小正方体码堆放成一个立体图,从上向下看这个立体图形,从正面看这个立体图形,所得图形如图所示,则这个立体图形的表面积最多是________.
48
分析:由从上向下看的图形可得最底层正方体的个数及正方体摆放的基本形状,由从正面看的图形可得第2层摆放几何体最多把俯视图中从左边数1,2,4列的正方体上都摆放几何体,进而按照上下,左右,前后方向计算该组合几何体的表面积即可.
解答:从上向下看的图形可得最底层正方体有8个正方体;
从正面看的图形可得第2层摆放几何体最多把俯视图中从左边数1,2,4列的正方体上都摆放几何体,共有5个正方体,
则从上面看可得到8个正方体,面积为8×12=8,
从正面看可得到8个正方体,面积为8×12=8,
从左面看露出正方体的面有8个,面积为6×12=6,
故这个立体的表面积最多为(8+8+6)×2+4=48.
故答案为:48.
点评:考查由视图判断几何体;用到的知识点为:俯视图中正方形的个数即为最底层正方体的个数;求组合几何体的面积应按照一定的规律求解.
分析:由从上向下看的图形可得最底层正方体的个数及正方体摆放的基本形状,由从正面看的图形可得第2层摆放几何体最多把俯视图中从左边数1,2,4列的正方体上都摆放几何体,进而按照上下,左右,前后方向计算该组合几何体的表面积即可.
解答:从上向下看的图形可得最底层正方体有8个正方体;
从正面看的图形可得第2层摆放几何体最多把俯视图中从左边数1,2,4列的正方体上都摆放几何体,共有5个正方体,
则从上面看可得到8个正方体,面积为8×12=8,
从正面看可得到8个正方体,面积为8×12=8,
从左面看露出正方体的面有8个,面积为6×12=6,
故这个立体的表面积最多为(8+8+6)×2+4=48.
故答案为:48.
点评:考查由视图判断几何体;用到的知识点为:俯视图中正方形的个数即为最底层正方体的个数;求组合几何体的面积应按照一定的规律求解.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 用一些棱长是1的小正方体堆成一个立体,从上往下看这个立体,如图,从前往后看(即从正面看)这个立体,如图,这些小立方体最少有多少个?
用一些棱长是1的小正方体堆成一个立体,从上往下看这个立体,如图,从前往后看(即从正面看)这个立体,如图,这些小立方体最少有多少个? 用一些棱长是1的小正方体码堆放成一个立体图,从上向下看这个立体图形,从正面看这个立体图形,所得图形如图所示,则这个立体图形的表面积最多是
用一些棱长是1的小正方体码堆放成一个立体图,从上向下看这个立体图形,从正面看这个立体图形,所得图形如图所示,则这个立体图形的表面积最多是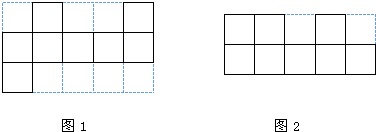 用一些棱长是1厘米的小正方体叠放成一个立体,从上向下看这个立体.(图1),从正面看这个立体(图2),则这个立体的体积是
用一些棱长是1厘米的小正方体叠放成一个立体,从上向下看这个立体.(图1),从正面看这个立体(图2),则这个立体的体积是 用一些棱长是1的小正方体堆成一个立体,从上往下看这个立体,如图,从前往后看(即从正面看)这个立体,如图,这些小立方体最少有多少个?
用一些棱长是1的小正方体堆成一个立体,从上往下看这个立体,如图,从前往后看(即从正面看)这个立体,如图,这些小立方体最少有多少个?