题目内容
15.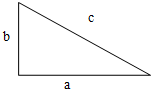 如图是一个边长分别为a、b、c的直角三角形,并且c2=a2+b2.请你分别以直角三角形的三边中点为圆心,以边长为直径在直角三角形外画半圆.这三个半圆面积是什么关系?并说明理由.
如图是一个边长分别为a、b、c的直角三角形,并且c2=a2+b2.请你分别以直角三角形的三边中点为圆心,以边长为直径在直角三角形外画半圆.这三个半圆面积是什么关系?并说明理由.
分析 先设直角三角形的三边分别为a、b、c,再由勾股定理及圆的面积公式即可得出三个半圆面积之间的关系.
解答 解:如图:
设直角三角形的三边分别为a、b、c,
则因为三个半圆的面积分别是:
$\frac{1}{2}$×π($\frac{a}{2}$)2=$\frac{1}{8}$πa2
$\frac{1}{2}$×π($\frac{b}{2}$)2=$\frac{1}{8}$πb2
所以$\frac{1}{8}$πa2+$\frac{1}{8}$πb2=$\frac{1}{8}$π(a2+b2)
而a2+b2=c2,
所以$\frac{1}{8}$πa2+$\frac{1}{8}$πb2=$\frac{1}{8}$πc2.
所以以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积.
点评 此题根据半圆的面积公式以及勾股定理证明:以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积,重在验证勾股定理.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
10.一个三位数,百位上的数字是a,十位上的数字是b,个位上的数字是5,表示这三位数的式子是( )
| A. | 100a+10b+5 | B. | a+b+5 | C. | a×b×5 |
