题目内容
大圆的半径与小圆的直径相等，大圆与小圆面积的比是 ．
考点：圆、圆环的面积,比的意义
专题：平面图形的认识与计算
分析：由“圆的面积=πr2”可知，圆的面积比就等于半径平方的比，再根据“大圆半径等于小圆直径”即可求得它们的面积比．
解答：
解：设小圆的半径为r，则大圆的半径2r；
则大圆面积：小圆面积=π（2r）2：πr2=4：1．
答：大圆与小圆面积的比是4：1．
故答案为：4：1．
则大圆面积：小圆面积=π（2r）2：πr2=4：1．
答：大圆与小圆面积的比是4：1．
故答案为：4：1．
点评：解答此题的关键是明白：圆的面积比就等于半径平方的比，设出未知数即可求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图反映的是小明每天上午从上学到放学回家的整过过程．从图中可以看出，从如图，图中小于平角的角是个数是（ ）
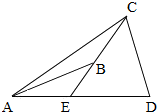
| A、9 | B、4 | C、11 | D、6 |
把40糖溶解在100克水中，求含糖率，正确的算式是（ ）
| A、40÷100 |
| B、（100-40）÷100 |
| C、40÷（40+100） |