题目内容
 一张长100厘米的长方形铁皮按图裁剪,正好能制成一只铁皮水桶,求所制成的水桶的容积(结果用含π的式子表示).
一张长100厘米的长方形铁皮按图裁剪,正好能制成一只铁皮水桶,求所制成的水桶的容积(结果用含π的式子表示).
解:设这个圆柱形水桶的底面半径是r厘米,根据题意可得方程:
2πr+2r=82.8,
(2π+2)r=100,
r= ,
,
所以这个圆柱的高是: ×4=
×4=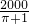 (厘米),
(厘米),
则这个水桶的容积是:π×( )2×
)2×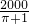 =
=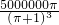 (立方厘米),
(立方厘米),
答:制成的水桶的容积是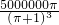 立方厘米.
立方厘米.
分析:要求这张铁皮的面积至少是多少平方分米,也就是求这个长方形的面积,这个长方形的宽是这两个圆的直径和,也就是4个半径,所以宽(即圆柱的高)=4×半径,长=底面周长+2×半径,设圆的半径是r,可得方程:2×πr+2r=100,由此即可求出半径的长度,再利用圆柱的容积=πr2h,计算出答案.
点评:解答本道题的关键是利用圆柱的侧面展开图的特点得出圆柱的底面半径与长方形的长和宽的关系解决问题.
2πr+2r=82.8,
(2π+2)r=100,
r=
 ,
,所以这个圆柱的高是:
 ×4=
×4=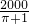 (厘米),
(厘米),则这个水桶的容积是:π×(
 )2×
)2×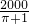 =
=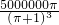 (立方厘米),
(立方厘米),答:制成的水桶的容积是
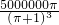 立方厘米.
立方厘米.分析:要求这张铁皮的面积至少是多少平方分米,也就是求这个长方形的面积,这个长方形的宽是这两个圆的直径和,也就是4个半径,所以宽(即圆柱的高)=4×半径,长=底面周长+2×半径,设圆的半径是r,可得方程:2×πr+2r=100,由此即可求出半径的长度,再利用圆柱的容积=πr2h,计算出答案.
点评:解答本道题的关键是利用圆柱的侧面展开图的特点得出圆柱的底面半径与长方形的长和宽的关系解决问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
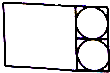 一张长100厘米的长方形铁皮按图裁剪,正好能制成一只铁皮水桶,求所制成的水桶的容积(结果用含π的式子表示).
一张长100厘米的长方形铁皮按图裁剪,正好能制成一只铁皮水桶,求所制成的水桶的容积(结果用含π的式子表示).