题目内容
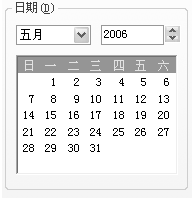 如图是2006年5月的台历,用“
如图是2006年5月的台历,用“ ”形框数,每次框住5个数.
”形框数,每次框住5个数.(1)如果框出的数最小是4,那么框出的5个数的平均数是多少?
(2)在右图中一共可以框出住
13
13
个不同的和.(3)如果框出的5个数中,必须有1个数在周三,那么有
7
7
种不同的框法.分析:(1)因为框住的数最小是4,所以框住的这5个数就是 4、10、11、12、18,由此求出它们的和再除以5即可;
(2)根据要求知道第一行、第二行与第三行可以框住5个不同的和,第二行、第三行与第四行可以框住5个不同的和,第三行、第四行与第五行可以框住3个不同的和,由此得出一共可以框住不同数的和的个数.
(3)根据要求知道,要使框出的5个数中,必须有1个数在周三,那么第一行、第二行与第三行有3种框法,第二行、第三行与第四行有3种框法;第三行、第四行与第五行有1种框法,由此得出一共有3+3+1=7种不同的框法.
(2)根据要求知道第一行、第二行与第三行可以框住5个不同的和,第二行、第三行与第四行可以框住5个不同的和,第三行、第四行与第五行可以框住3个不同的和,由此得出一共可以框住不同数的和的个数.
(3)根据要求知道,要使框出的5个数中,必须有1个数在周三,那么第一行、第二行与第三行有3种框法,第二行、第三行与第四行有3种框法;第三行、第四行与第五行有1种框法,由此得出一共有3+3+1=7种不同的框法.
解答:解:(1)(4+10+11+12+18)÷5,
=55÷5,
=11;
(2)因为第一行、第二行与第三行可以框住5个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住3个不同的和,
所以一共可以框住不同数的和的个数是:5+5+3=13,
(3)要使框出的5个数中,必须有1个数在周三,那么第一行、第二行与第三行有3种框法,
第二行、第三行与第四行有3种框法;
第三行、第四行与第五行有1种框法,
由此得出一共有3+3+1=7种不同的框法.
答:(1)如果框住的数最小是4,那么框住的5个数的平均数是11,
(2)一共可以框住13个不同数的和.
(3)框出的5个数中,必须有1个数在周三,那么有7种不同的框法.
故答案为:13;7.
=55÷5,
=11;
(2)因为第一行、第二行与第三行可以框住5个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住3个不同的和,
所以一共可以框住不同数的和的个数是:5+5+3=13,
(3)要使框出的5个数中,必须有1个数在周三,那么第一行、第二行与第三行有3种框法,
第二行、第三行与第四行有3种框法;
第三行、第四行与第五行有1种框法,
由此得出一共有3+3+1=7种不同的框法.
答:(1)如果框住的数最小是4,那么框住的5个数的平均数是11,
(2)一共可以框住13个不同数的和.
(3)框出的5个数中,必须有1个数在周三,那么有7种不同的框法.
故答案为:13;7.
点评:解答此题的关键是,根据台历表和所框的要求,由框住的数最小是4,确定其它的四个数,再根据求平均数的方法解答;分情况找出框住不同数的和的个数即可.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
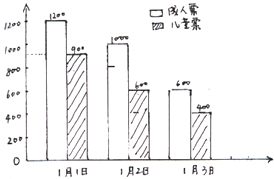 洪山公园2006年元旦售票情况如图.
洪山公园2006年元旦售票情况如图.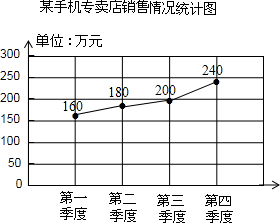 (2006?江阴市)选择你喜欢的方法解答下列问题
(2006?江阴市)选择你喜欢的方法解答下列问题