题目内容
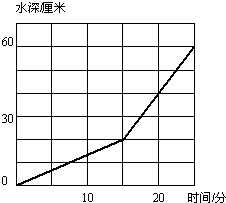 长、宽、高分别为80厘米、60厘米、70厘米的长方体水箱中装有A,B 两个进水管,先开B管,过一段时间后两管齐开.下边的折线统计图表示进水情况.
长、宽、高分别为80厘米、60厘米、70厘米的长方体水箱中装有A,B 两个进水管,先开B管,过一段时间后两管齐开.下边的折线统计图表示进水情况.①
15
15
分钟后A,B两管同时开放,这时水深是20
20
厘米.②A,B两管同时进水,每分钟进水
19200
19200
毫升.分析:①从统计图中可以看出,15分钟后,每分钟的进水量增多了,说明15分钟后A、B两管同时开放,这时水深是20厘米;
②要求A、B两管同时进水,每分钟进水的体积,首先应求出每分钟进水的深度,然后根据长方体体积公式即可解决.
②要求A、B两管同时进水,每分钟进水的体积,首先应求出每分钟进水的深度,然后根据长方体体积公式即可解决.
解答:解:①(15)分钟后A,B两管同时开放,这时水深是(20)厘米.
②每分钟进水深度:
(60-20)÷(25-15),
=40÷10,
=4(厘米);
每分钟进水体积:
80×60×4=19200(毫升);
答:每分钟进水19200毫升.
故答案为:15,20,19200.
②每分钟进水深度:
(60-20)÷(25-15),
=40÷10,
=4(厘米);
每分钟进水体积:
80×60×4=19200(毫升);
答:每分钟进水19200毫升.
故答案为:15,20,19200.
点评:此题首先根据问题从图中找出所需要的信息,然后根据长方体体积公式V=abh即可解决.

练习册系列答案
相关题目
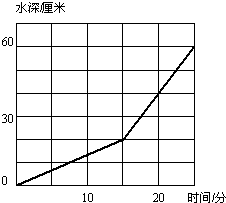 长、宽、高分别为80厘米、60厘米、70厘米的长方体水箱中装有A,B 两个进水管,先开B管,过一段时间后两管齐开.下边的折线统计图表示进水情况.
长、宽、高分别为80厘米、60厘米、70厘米的长方体水箱中装有A,B 两个进水管,先开B管,过一段时间后两管齐开.下边的折线统计图表示进水情况.