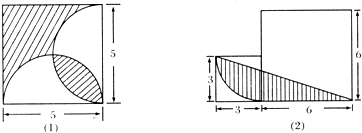
题目内容
解:(1)5×5× ,
,
=25× ,
,
=12.5;
答:阴影部分的面积是12.5.
(2)(3+6)×3÷2-(3×3- ×3.14×32),
×3.14×32),
=9×3÷2-(9-7.065),
=27÷2-1.935,
=13.5-1.935,
=11.565;
答:阴影部分的面积是11.565.
分析:如图所示:(1)易知两段半圆的交点即为正方形的对称中心(设为O),连接OC、BD;将两个弓形分别进行旋转,即可将所求的阴影部分的面积转化为半个正方形的面积,即,将阴影③、④分别旋转到空白①、②的位置,即可得解.
(2)阴影部分的面积=三角形ABE的面积-空白①的面积,三角形ABE的底是(3+6)米,高等于小正方形的边长,于是可以求其面积,空白①的面积等于小正方形的面积减去以小正方形的边长为半径的圆的面积的 ,从而可以求出阴影部分的面积.
,从而可以求出阴影部分的面积.
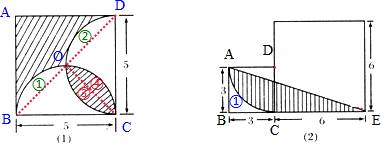
点评:(1)解答此题的关键是作出辅助线,利用旋转的方法,得出阴影部分的面积等于正方形面积的一半,从而问题得解.
(2)明白:阴影部分的面积=三角形ABE的面积-空白①的面积,是解答本题的关键.
 ,
,=25×
 ,
,=12.5;
答:阴影部分的面积是12.5.
(2)(3+6)×3÷2-(3×3-
 ×3.14×32),
×3.14×32),=9×3÷2-(9-7.065),
=27÷2-1.935,
=13.5-1.935,
=11.565;
答:阴影部分的面积是11.565.
分析:如图所示:(1)易知两段半圆的交点即为正方形的对称中心(设为O),连接OC、BD;将两个弓形分别进行旋转,即可将所求的阴影部分的面积转化为半个正方形的面积,即,将阴影③、④分别旋转到空白①、②的位置,即可得解.
(2)阴影部分的面积=三角形ABE的面积-空白①的面积,三角形ABE的底是(3+6)米,高等于小正方形的边长,于是可以求其面积,空白①的面积等于小正方形的面积减去以小正方形的边长为半径的圆的面积的
 ,从而可以求出阴影部分的面积.
,从而可以求出阴影部分的面积.
点评:(1)解答此题的关键是作出辅助线,利用旋转的方法,得出阴影部分的面积等于正方形面积的一半,从而问题得解.
(2)明白:阴影部分的面积=三角形ABE的面积-空白①的面积,是解答本题的关键.

练习册系列答案
相关题目