题目内容
一个圆环,内圆半径是外圆半径的 ,这个圆环的面积是内圆面积的
,这个圆环的面积是内圆面积的
- A.3倍
- B.
 倍
倍 - C.
 倍
倍 - D.
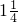 倍
倍
A
分析:设内圆半径为r,则外圆半径为2r,圆环的面积=大圆的面积-小圆的面积,再求出内圆的面积,即可进行比较.
解答:设内圆半径为r,则外圆半径为2r;
因为圆环面积=π(2r)2-πr2=4πr2-πr2=3πr2,
所以圆环面积:内圆的面积=3πr2:πr2=3;
答:这个圆环的面积是内圆面积的3倍.
故选:A.
点评:解答本题时,应先求出圆环的面积,再与内圆的面积比较即可.
分析:设内圆半径为r,则外圆半径为2r,圆环的面积=大圆的面积-小圆的面积,再求出内圆的面积,即可进行比较.
解答:设内圆半径为r,则外圆半径为2r;
因为圆环面积=π(2r)2-πr2=4πr2-πr2=3πr2,
所以圆环面积:内圆的面积=3πr2:πr2=3;
答:这个圆环的面积是内圆面积的3倍.
故选:A.
点评:解答本题时,应先求出圆环的面积,再与内圆的面积比较即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是3cm,圆环面积是
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是3cm,圆环面积是