题目内容
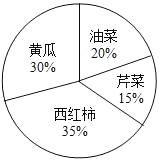
【题目】图中两个正方形的面积相差400平方厘米，则圆A与圆B的面积相差多少？
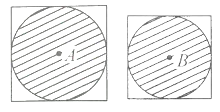
【答案】314cm2
【解析】
本题可以用假设法作答，可以设大圆半径为R，小圆半径为r，由此得出：SA-SB=πR2-πr2=π（R2-r2），S大正方形-S小正方形=2R×2R-2r×2r=4（R2-r2），因为题中已经告诉了两个正方形的面积之差，所以4（R2-r2）=400，R2-r2=100，然后代入π（R2-r2）作答即可。
假设大圆半径为R，小圆半径为r。
SA-SB=πR2-πr2=π（R2-r2）
因为S大正方形-S小正方形=2R×2R-2r×2r=4（R2-r2）=400，
所以R2-r2=100，
所以圆A与圆B的面积相差3.14×100=314（cm2）
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了调查学生对雾霾天气知识的了解程度，某校在学生中作了一次抽样调查，将调查情况分为A、B、C、D四个等级，调查结果如下面图表。
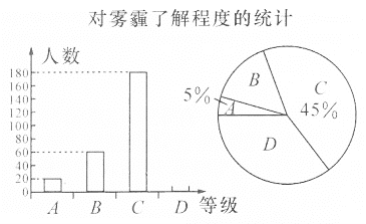
了解程度 | 百分比 |
| 5% |
| m% |
| 45% |
| n% |
据统计图表，回答下列问题：
（1）表格中m=________%，n=________%。
（2）图所表示的扇形统计图中D部分扇形所对应的圆心角是________度。
（3）调查结果为D等（不了解雾霾知识）人数是________人。
