题目内容
A、B两人同时从700米长的山坡坡底出发向上跑,跑到坡顶立即返回.他们俩的上坡速度不同,下坡速度则是两人各自上坡速度的二倍.B首先到达坡顶,立即沿原路返回,并且在离坡顶70米处与A相遇.当B到达坡底(注:起点)时,那么A落后B________米.
300
分析:B在离坡顶70米处与A相遇,由于下坡速度是两人各自上坡速度的二倍,那么B下坡70米就相当于上坡行驶70÷2=35米,即两人相遇时(按照上坡速度),相当于A走了700-70=630米,B走了700+35=735米,据此可求出两人上坡的速度比(7:6),当两人相遇后,A又走了70米到达山顶,在此时间里(BA的速度比就是7:3)B就走了70× =
= 千米,也就是说当A到达山顶时,B距离坡底还有700-70-
千米,也就是说当A到达山顶时,B距离坡底还有700-70- =
= 米,然后两人同时以下坡的速度下坡(以7:6速度下坡),当B跑完
米,然后两人同时以下坡的速度下坡(以7:6速度下坡),当B跑完 米时,A跑了
米时,A跑了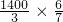 =400米,最后根据A落后B距离=山坡的长度-A下山距离即可解答.
=400米,最后根据A落后B距离=山坡的长度-A下山距离即可解答.
解答:相遇时换算成上坡时B行驶的路程:
700+70÷2,
=700+35,
=735(米),
A行驶的路程:
700-70=630(米),
两人上坡时的速度比:
735:630=7:6,
A到达山顶时B与坡底的距离:
700-70-70× 2,
2,
=700-70- ,
,
= (米),
(米),
B到达坡底时,A跑的距离:
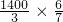 =400(米),
=400(米),
700-400=300(米),
答:A落后B300米,
故答案为:300.
点评:本题属于比较难的应用题,求出两人的速度比非常重要,只有求出两人的速度比,才能根据时间一定,路程和速度成正比,求出当B到达坡底时,A下坡跑的距离.
分析:B在离坡顶70米处与A相遇,由于下坡速度是两人各自上坡速度的二倍,那么B下坡70米就相当于上坡行驶70÷2=35米,即两人相遇时(按照上坡速度),相当于A走了700-70=630米,B走了700+35=735米,据此可求出两人上坡的速度比(7:6),当两人相遇后,A又走了70米到达山顶,在此时间里(BA的速度比就是7:3)B就走了70×
 =
= 千米,也就是说当A到达山顶时,B距离坡底还有700-70-
千米,也就是说当A到达山顶时,B距离坡底还有700-70- =
= 米,然后两人同时以下坡的速度下坡(以7:6速度下坡),当B跑完
米,然后两人同时以下坡的速度下坡(以7:6速度下坡),当B跑完 米时,A跑了
米时,A跑了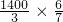 =400米,最后根据A落后B距离=山坡的长度-A下山距离即可解答.
=400米,最后根据A落后B距离=山坡的长度-A下山距离即可解答.解答:相遇时换算成上坡时B行驶的路程:
700+70÷2,
=700+35,
=735(米),
A行驶的路程:
700-70=630(米),
两人上坡时的速度比:
735:630=7:6,
A到达山顶时B与坡底的距离:
700-70-70×
 2,
2,=700-70-
 ,
,=
 (米),
(米),B到达坡底时,A跑的距离:
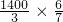 =400(米),
=400(米),700-400=300(米),
答:A落后B300米,
故答案为:300.
点评:本题属于比较难的应用题,求出两人的速度比非常重要,只有求出两人的速度比,才能根据时间一定,路程和速度成正比,求出当B到达坡底时,A下坡跑的距离.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目