题目内容
2.有三堆棋子,数目相等,每堆至少有4枚,从左堆中取出3枚放入中堆,从右堆中取出4枚放入中堆,再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,这时中堆的棋子数是多少?请做一做,并解释其中的道理.分析 设三堆棋子各有x枚,从左堆中取出3枚放人中堆,左堆中还剩下(x-3)枚,此时右堆中有(x+3)枚;从右堆中取出4枚放人中堆,此时右堆中有(x+3+4)枚;再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,从中堆中取出的数量为(x-3)枚,这时中堆的棋子数是(x+3+4)-(x-3).
解答 解:设三堆棋子各有x枚,
(x+3+4)-(x-3)
=(x+7)-x+3
=7+3
=10(枚)
答:这时中堆的棋子数是10枚.
点评 此题解答的关键在于抓住“有三堆棋子,数目相等”,设出三堆棋子各有x枚,根据取、放的棋子数量进行推导,解决问题.

练习册系列答案
相关题目
13.用简便方法计算.
| 31+67+69 | 638+297-197 | 436-99 |
| 545+211+189+155 | 962-(362+139) | 526-57-43-26 |
14.某实验小学四年级开展书法作品评选活动,下面是四年级4个班的获奖情况.
(1)把上表填写完整.
(2)比较上表中各个分数的大小,并将它们按从小到大的顺序排起来.
| 班级 | 四(1)班 | 四(2)班 | 四(3)班 | 四(4)班 |
| 获奖作品 | 8 | 7 | 12 | 9 |
| 参赛作品 | 10 | 14 | 18 | 12 |
| 获奖作品占参赛作品的几分之几 |
(2)比较上表中各个分数的大小,并将它们按从小到大的顺序排起来.
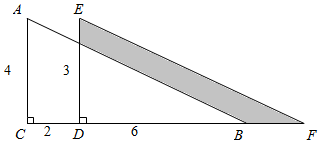 三角形ABC和三角形EFD是两个完全相同的直角三角形.把它们的个部分叠放在一起,如图所示.求阴影部分的面积.(单位:cm)
三角形ABC和三角形EFD是两个完全相同的直角三角形.把它们的个部分叠放在一起,如图所示.求阴影部分的面积.(单位:cm)