题目内容
9.下面的正方体、圆柱体和圆锥等底等高,判断正确的是( )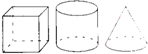
| A. | 它们的体积都相等 | B. | 圆柱体的体积最大 | ||
| C. | 圆锥的体积是正方体的$\frac{1}{3}$ |
分析 首先根据正方体的体积=底面积×高,圆柱的体积=底面积×高,可得等底等高的正方体的体积等于圆柱的体积;然后根据圆锥的体积等于与它等底等高的圆柱体体积的$\frac{1}{3}$,可得等底等高的圆锥的体积是正方体的$\frac{1}{3}$,所以等底等高的正方体、圆柱体和圆锥中,圆柱体和正方体的体积相等,圆锥的体积最小,据此判断即可.
解答 解:因为正方体的体积=底面积×高,圆柱的体积=底面积×高,
所以等底等高的正方体的体积等于圆柱的体积,
又因为圆锥的体积等于与它等底等高的圆柱体体积的$\frac{1}{3}$,
所以圆锥的体积等于与它等底等高的正方体体积的$\frac{1}{3}$,
所以等底等高的正方体、圆柱体和圆锥中,圆柱体和正方体的体积相等,圆锥的体积最小.
故选:C.
点评 此题主要考查了圆柱、圆锥的体积的求法,以及正方体的体积的求法,要熟练掌握,解答此题的关键是要明确:等底等高的正方体、圆柱体和圆锥中,圆柱体和正方体的体积相等,圆锥的体积最小.

练习册系列答案
相关题目
1.直接写出得数.
| 13×4= | 28×3= | 30×2= | 55÷5= | 7×40= |
| 20×50= | 143-70= | 11×4= | 23+60= | 80×17×0= |
18.如果a×$\frac{1}{3}$=b×$\frac{1}{4}$(a、b两数都大于0),a与b比较( )
| A. | a>b | B. | a<b | C. | a=b |