Question

某校有100名学生到离学校33千米的郊区参加采摘活动，学校只有一辆限乘25人的中型面包车，为了让全体学生尽快地到达目的地，决定采取步行与乘车相结合的办法．已知学生步行的速度是每小时5千米，汽车行驶的速度是每小时55千米．请你设计一个方案，使全体学生都能到达目的地的最短时间是多少小时？

Answer 1

分析：如图：由于汽车的速度是人行速度的55÷5=11倍，那么其中一组同学走一段的路程，汽车一来一回应走同样的11段路程．出发时，第一组乘车，其他三组同学步行．当汽车行到某处返回接第二组同学时，人和车应走12段的路程．
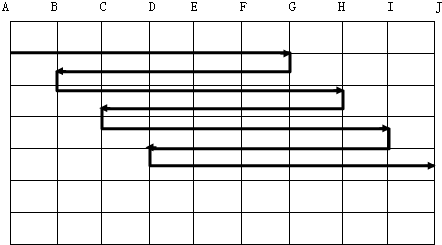
整体考虑，步行走了一段路程，即图中AB，汽车走了11段路程（图中AG+GB）．人和车总是这样不停地行走，就会同时到达终点．根据这个方案，学校到采摘园的路程就被平均分成了9份，汽车共行了这样的39份路程，那么题目隐藏的条件也就出现了：一段路程×9=33．根据这个条件，可挖掘出等量关系：汽车速度×时间=汽车行39段的路程．
33÷9×39÷55=2.6（小时）．

解答：解：汽车的速度是步行的：
55÷5=11（倍）；
学生需要分成：
100÷25=4（组）．
如要在最短的时间内到达，应使汽车与行人使终在运动，中间不停留且同时到达目的地，由此可设计如下方案：
如图：

发时，第一组乘车，其他三组同学步行．当汽车行到某处返回接第二组同学时，人和车应走12段的路程．
整体考虑，步行走了一段路程，即图中AB，汽车走了11段路程（图中AG+GB）．
人和车总是这样不停地行走，就会同时到达终点．
根据这个方案，学校到采摘园的路程就被平均分成了9份，汽车共行了这样的39份路程，那么题目隐藏的条件也就出现了：一段路程×9=33．可得等量关系：汽车速度×时间=汽车行39段的路程．
即：33÷9×39÷55=2.6（小时）．
答：全体学生都能到达目的地的最短时间是2.6小时．

点评：明确如要在最短的时间内到达，应使汽车与行人使终在运动，中间不停留且同时到达目的地，并根据汽车与步行的速度比画图得出数量之间的关系是完成本题的关键．