题目内容
直角三角形的两个锐角的比是2：3，则较大的那个锐角的度数是________．
54°
分析：依据三角形的内角和是180°可得：直角三角形的两个锐角的和是90°，两个锐角的比已知，于是利用按比例分配的方法，即可求出较大的锐角的度数．
解答：两个锐角的和：180°-90°=90°，
90°×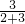
=54°；
故答案为：54°．
点评：解答此题的主要依据是：直角三角形的角的特点以及三角形的内角和定理．
分析：依据三角形的内角和是180°可得：直角三角形的两个锐角的和是90°，两个锐角的比已知，于是利用按比例分配的方法，即可求出较大的锐角的度数．
解答：两个锐角的和：180°-90°=90°，
90°×
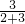=54°；故答案为：54°．
点评：解答此题的主要依据是：直角三角形的角的特点以及三角形的内角和定理．
练习册系列答案
阅读快车系列答案
相关题目