题目内容
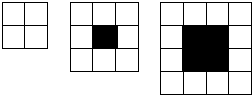如图那样用边长为10厘米的正方形纸板拼图（正方形），要求四周白色，中间黑色．如果每边放6块，共需几块白纸板？请继续画草图，并填表：
| 每边白正方形 | 2 | 3 | 4 | 5 | 6 | … | 25 | … |
| 中间黑正方形 | 0 | 1 | 4 | … | … |
分析：观察图形可知，每边白正方形的个数与中间的黑色正方形的个数之间的关系是：如果每边白正方形的个数是n，则黑色正方形的个数就是（n-2）2；据此即可解答．
解答：解：根据题干分析可得，每边白正方形的个数与中间的黑色正方形的个数之间的关系是：
如果每边白正方形的个数是n，则黑色正方形的个数就是（n-2）2；
当n=5时，黑色正方形有：（5-2）2=9（个）；
当n=6时，黑色正方形有：（6-2）2=16（个）；
当n=25时，黑色正方形有：（25-2）2=529（个）；
据此可以把上表填充完整如下：
如果每边白正方形的个数是n，则黑色正方形的个数就是（n-2）2；
当n=5时，黑色正方形有：（5-2）2=9（个）；
当n=6时，黑色正方形有：（6-2）2=16（个）；
当n=25时，黑色正方形有：（25-2）2=529（个）；
据此可以把上表填充完整如下：
点评：主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．
练习册系列答案
相关题目
如图那样用边长为10厘米的正方形纸板拼图（正方形），要求四周白色，中间黑色．如果每边放6块，共需几块白纸板？
请继续画草图，并填表：
| 每边白正方形 | 2 | 3 | 4 | 5 | 6 | … | 25 | … |
| 中间黑正方形 | 0 | 1 | 4 | … | … |