Question

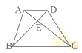
【题目】如下图，AC，BD是梯形ABCD的对角线，三角形ABC与三角形（___）的面积一定相等；三角形DEC与三角形（___）的面积一定相等。

Answer 1

【答案】△DBC △AEB

【解析】

通过已知条件图形分析可知：△ABC与△DBC同底等高；△ABD与△ACD同底等高,即△DEC＋△DEA=△AEB＋△DEA根据等式性质据此解答即可。

通过观察图形可知：△ABC与△DBC同底（BC）等高（梯形的高），所以△ABC=△DBC；

△ABD与△ACD同底（AD）等高（梯形的高）,所以△ABD=△ACD根据等式性质得: △DEC＋△DEA=△AEB＋△DEA，即△DEC =△AEB。

故正确答案是三角形ABC与三角形DBC的面积一定相等；三角形DEC与三角形AEB的面积一定相等。