题目内容
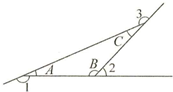 如图,三角形三个内角分别为∠A、∠B、∠C,外角分别为∠1、∠2、∠3,已知:∠A+∠B+∠C=180°,∠A=∠C.
如图,三角形三个内角分别为∠A、∠B、∠C,外角分别为∠1、∠2、∠3,已知:∠A+∠B+∠C=180°,∠A=∠C.
(1)∠1、∠2、∠3中有相等的角吗?______.
(2)求∠1+∠2+∠3=______.
解:(1)因为∠1+∠A=∠3+∠C=180°,∠A=∠C,所以∠1=∠3;
(2)因为(∠A+∠1)+(∠B+∠2)+(∠C+∠3)=180°×3=540°,
其中∠A+∠B+∠C=180°,所以∠1+∠2+∠3=540-(∠A+∠B+∠C)=360°;
故答案为:∠1=∠3,360°.
分析:(1)因为平角=180度,∠1+∠A=∠3+∠C=180°,∠A=∠C,所以∠1=∠3;
(2)因为平角的度数是180度,(∠A+∠1)+(∠B+∠2)+(∠C+∠3)=180°×3=540°,三角形的内角和是180度,即∠A+∠B+∠C=180°,所以∠1+∠2+∠3=540-(∠A+∠B+∠C)=360°;据此解答.
点评:明确平角的含义,灵活掌握三角形的内角和是18-度,是解答此题的关键.
(2)因为(∠A+∠1)+(∠B+∠2)+(∠C+∠3)=180°×3=540°,
其中∠A+∠B+∠C=180°,所以∠1+∠2+∠3=540-(∠A+∠B+∠C)=360°;
故答案为:∠1=∠3,360°.
分析:(1)因为平角=180度,∠1+∠A=∠3+∠C=180°,∠A=∠C,所以∠1=∠3;
(2)因为平角的度数是180度,(∠A+∠1)+(∠B+∠2)+(∠C+∠3)=180°×3=540°,三角形的内角和是180度,即∠A+∠B+∠C=180°,所以∠1+∠2+∠3=540-(∠A+∠B+∠C)=360°;据此解答.
点评:明确平角的含义,灵活掌握三角形的内角和是18-度,是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
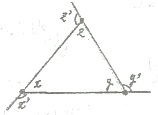 如图,x′,y′,z′和x,y,z分别是三角形的三个外角和三个内角,若x′:y′:z′=4:5:6,则x:y:z=
如图,x′,y′,z′和x,y,z分别是三角形的三个外角和三个内角,若x′:y′:z′=4:5:6,则x:y:z=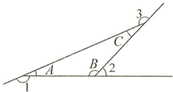 如图,三角形三个内角分别为∠A、∠B、∠C,外角分别为∠1、∠2、∠3,已知:∠A+∠B+∠C=180°,∠A=∠C.
如图,三角形三个内角分别为∠A、∠B、∠C,外角分别为∠1、∠2、∠3,已知:∠A+∠B+∠C=180°,∠A=∠C.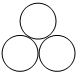 (2008?扬州)如图是由三个半径相等的圆组成的平面图形,它有
(2008?扬州)如图是由三个半径相等的圆组成的平面图形,它有 如图,等边三角形的一条高把它分成两个三角形,其中一个三角形三个内角的度数分别是
如图,等边三角形的一条高把它分成两个三角形,其中一个三角形三个内角的度数分别是