题目内容
【题目】在平面直角坐标系xOy中，已知点B(1,0)，圆A：(x＋1)2＋y2＝16，动点P在圆A上，线段BP的垂直平分线与AP相交于点Q，设动点Q的轨迹为曲线C.
(1)求曲线C的方程；
(2)过点B(1,0)且斜率为1的直线与曲线C相交于E，F两点，求弦长|EF|．
【答案】(1) 
．(2) 
．
【解析】试题分析：（1）由垂直平分线的性质可得
在线段
上，所以
，利用椭圆的定义，可求曲线
的方程；（2）求出
的方程，联立直线与椭圆方程，设出义
坐标，通过韦达定理以及弦长公式即可求解
的距离.
试题解析：(1)由已知|QP|＝|QB|，Q在线段PA上，所以|QA|＋|QB|＝|AQ|＋|QP|＝4，
所以点Q的轨迹是椭圆，2a＝4，a＝2,2c＝2，c＝1，
所以b2＝3，
曲线C的方程为
＋
＝1．
(2)直线EF的方程为：y＝x－1．
由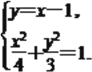
消去y整理得7x2－8x－8＝0，
设E(x1，y1)，F(x2，y2)，
所以x1＋x2＝
，x1·x2＝－，
|EF|＝
·
＝
·
＝
．
练习册系列答案
名校课堂系列答案
相关题目
