题目内容
10个钉组成的正三角点阵中，用橡皮筋可套出 个三角形．
考点：组合图形的计数
专题：几何的计算与计数专题
分析：10个钉组成的正三角点阵如下图，
先用线段把相邻的点连起来，再分类计数：边长为1的正三角形、边长为2的正三角形、边长为3的正三角形，个数相加即可．
先用线段把相邻的点连起来，再分类计数：边长为1的正三角形、边长为2的正三角形、边长为3的正三角形，个数相加即可．
解答：
解：如图所示，
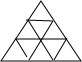
边长为1的正三角形共有1+3+5=9个；
边长为2的正三角形共有3个；
边长为3的正三角形共有1个．
综上可知：共有9+3+1=13个．
故答案为：13．
边长为1的正三角形共有1+3+5=9个；
边长为2的正三角形共有3个；
边长为3的正三角形共有1个．
综上可知：共有9+3+1=13个．
故答案为：13．
点评：本题考查了计数问题，注意分类计数方法的运用．
练习册系列答案
天天向上口算本系列答案
相关题目